Rock Paper Scissors is a Game of Skill

Its strategy guide is the human mind

Games fall along a continuum of skill-based and luck-based. Some games, like War, are purely luck-based and involve no choices. Others are purely skill-based, like Chess, in that there’s no hidden information and the player is presented with a choice on each turn.

The question came up during Inkhaven of where rock-paper-scissors (RPS) falls on this spectrum. At first, I thought RPS was a game of 90% luck and 10% skill. After all, maybe you can intuit your opponent’s leading move from their personality, and maybe you can pick up on a few patterns, but surely it’s largely the luck of the draw, right?

Right?

In some sense this is true. RPS is a symmetric game in which each move is game-theoretically identical to every other. We can see this in the payoff matrix:

The first column represents Player 1’s choices, the first row represents Player 2’s. The first number in each cell represents the payoff for Player 1, the second number represents the payoff for Player 2. If you do the minmax on this table you’ll see that there’s no pure Nash equilibrium. For both players, all strategies are equivalent, which means the optimal strategy is to play each move 33% of the time at random. This is known as a mixed-strategy Nash equilibrium. If two rational players meet in a tournament, whoever wins their best-out-of-five match will be a matter of chance.

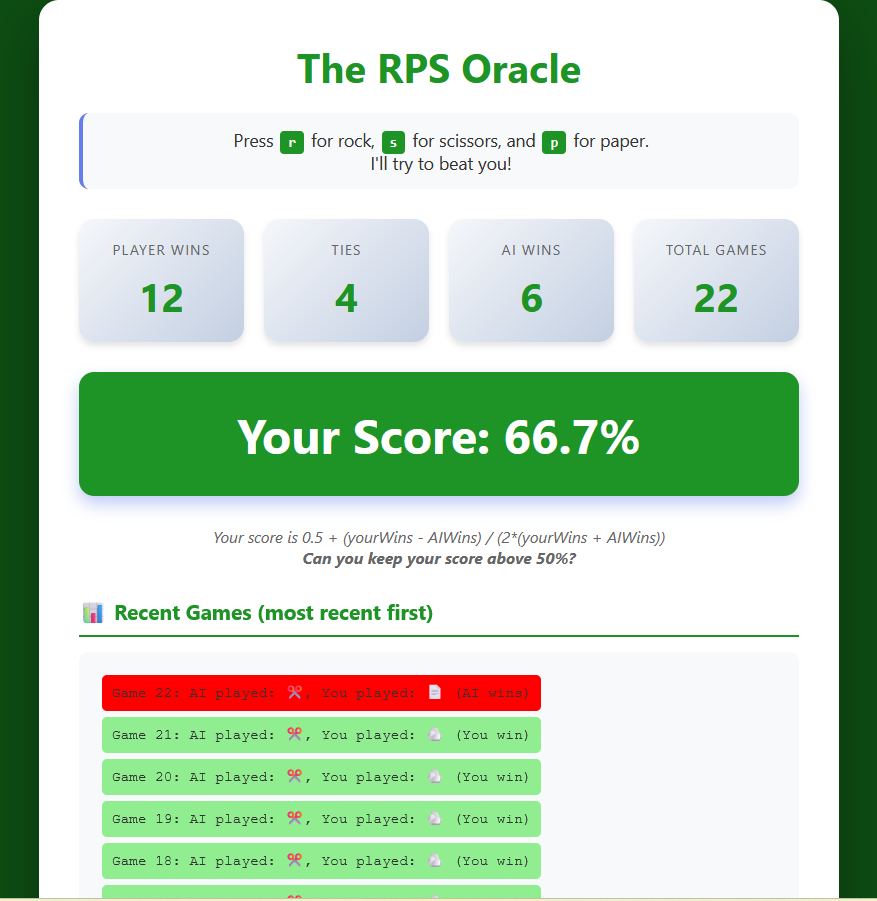
Armed with this knowledge, I encourage you to test your RPS mettle. I coded a little app that lets you play repeated RPS games against an AI. See how long you can keep your win rate above 50%.

Rock rocks!!! Play rock by pressing p, scissors by pressing s, and paper by pressing p.

You may notice that it gets more difficult to consistently win against the AI over time — after 120 games, I’ve seen few people keep their scores above 60%. Why is this?

I encourage you to form your own hypotheses. The answer will be below the spacer.

---

…

…

…

…

The Oracle’s Answer

Humans can’t achieve the RPS mixed Nash equilibrium because we can’t generate random numbers. The closest humans come is pseudorandomness, a pattern of random-looking results from the subconscious mind. Any half-decent AI can pick up on its underlying patterns and use them to their advantage.

Humans have certain biases when playing RPS. In a 2014 Chinese paper, a team of scientists documented these over the course of over 100,000 RPS games.

The simplest pattern is that players show a bias towards rock, possibly since it’s the easiest to form, as the count to three is typically conducted with both players making a fist. The AI takes advantage of this by leading with scissors.

After the first round, players show two tendencies:

1. If they lose, in the next game they tend to throw whatever beat them last round. For example, if they lost with rock against paper, they will most likely play paper next round.

2. If the player wins, they show a bias toward sticking with what they won with last time. So if a player won with rock against scissors, they’ll likely go with rock on the second trial.

These are the rules the oracle uses for the first five games. If the oracle wins against a player, they’ll play what beats their last pick in order to counteract rule 1. If the oracle loses, it’ll play what beats the last player’s pick to take advantage of rule 2. These are both good strategies to choose if you win against casual RPS players.

After these first few trials, the oracle shifts to a more sophisticated strategy. It records the user’s entire play history as a sliding sequence of five grams, like [RPSSP] or [PRSPR]. These are entered as the keys to a dictionary. Their values are the count of how many of each type the player threw after each five-gram.

For example, if the player has played the sequence RPSSSRSPR, the dictionary would look like the following:

[RPSSS]: {R: 1, P: 0, S: 0}

[PSSSR]: {R; 0, P: 0, S: 1}

[SSSRS]: {R: 0, P: 1, S: 0}

[SSRSP]: {R: 1, P: 0, S: 0}

Over time these five-grams repeat and the AI gets better at playing against the user. The AI chooses whatever would beat the action the player will most likely throw after the current five-gram.

This RPS oracle is an expansion on this implementation of the Aaronson Oracle by Nick Merrill. It doesn’t do quite as well as the Aaronson oracle because there are three choices rather than two: using multiple layers of n-grams would likely result in an improvement, as well as other heuristics to break ties. Rome wasn’t built in a day, and neither can be the optimal RPS strategy.